中学受験プロ教師の【受験算数】 vol.7 〜SAPIXなど進学塾に通う皆さんは必見！〜
カテゴリ : 中学受験, 中学受験プロ教師の【受験算数】
段々と暖かくなってきました。気温が上がってくると水分補給が重要になってきます。
勉強の合間に水分補給でリフレッシュ等はいかがでしょうか。
というわけで、前回（ブログvol.６＜４/２１号＞）の水の問題はどうでしたか？
底面積の変化の問題としてはやや難しいといったところでしょうか。
ただ、ひとつだけヒントの出し方にトラップを仕掛けておきました。
それは水位についてで、①＝１０ｃｍ、②はヒントなし、③＝（②－２）ｃｍとなっている所です。
じつは、①＝②は明らかなので、③＝８ｃｍと簡単に求められるのですが、諦めてしまった人もいたのではないでしょうか。
やはり問題文をよく読むことが基本中の基本になります。
「読む」といってもただ字面を追うのではなく、内容を自分の中に取り込まなければなりません。
そのためには、どうしても「図」や「表」のようなものを書き、それを見ながら考えることが必要となります。
また、「粘り」も試験においては重要です。
色々試しているうちに偶然、正解を見つけることもあります。
諦めてしまえば可能性は０（ゼロ）です。
少しずつで良いので、粘りの姿勢を身に着けていきましょう。
前回に引き続き「立体図形」がテーマです。
まずは、テーマ別のポイントを確認しましょう。
| 多面体 | 正多面体五種類は十分に学習しておきましょう。特に四・六・八に関しては頂点、辺、面の数がわかるのは勿論のこと、性質等も頭に入れておいてください。名前は覚えなくてもよいですが、切頂四面体や立方八面体等も押さえておくと良いでしょう。 |
|---|---|
| 立方体の切断 | 立体切断は立体の中でも難解と思われがちですが、基本から積み上げていけばむしろ取り組みやすい分野だと思います。立方体を平面で切ったとき、切り口として考えられるのは三角形、 四角形、五角形、六角形です。学習の際は当然もっと細かく分類する必要があります。例えば四角形は①台形②等脚台形 ③平行四辺形④ひし形⑤長方形⑥正方形が考えられます。 切り方と切り口の形の関係はしっかり確認しておきましょう。 |
| 立方体の積木 | 小立方体を集めて大きな立体を作る問題は、立方体を重ねるだけでなく、くりぬいたり切断したり、いろいろな問題が考えられます。「輪切り方式」や「上から見て何段重ねか」等平面で処理するやり方をマスターしておきましょう。立方体の積木の場合、表面積は「３方向の面積の和×２ 」で求められますが、凹みがある場合は少し注意が必要です。 |
| 投影図(推理) | 投影図から得られる情報は完全ではないことがあります。その場合、いろいろな立体が考えられるので、確定している部分と不確定の部分を明確にすることが大切です。 |
立体図形で一番ネックになっていることは、出題されるのは紙の上だということです。
解くのも当然紙の上ですよね。
つまり３次元のものを、２次元で表現したもので与えられ、それを頭の中はともかく、２次元である紙の上で解かなければならないのです。
苦手にする生徒さんが多いのも当然かもしれません。
「苦手からの脱出法」は、まず立体のイメージをつかむことです。
これは実際に立体を目にし、手に取るのが良いでしょう。
私は、自分が担当した生徒さんに相当数の立体を作って見せてきました。
実物を見た後は立体図形に対する恐怖感が薄れるケースが多かったように思います。
次に「３次元⇔２次元」を対応させる練習をすることです。
「輪切り方式」が典型的ですが、立体のままでは大変でも平面で考えればなんとかなるものです。
最後に知識の充実を挙げておきます。
立体図形は他の分野に比べ範囲が狭いといえます。
ですから学習すればするほど「既視感」のある問題に当たる可能性が高くなります。
「知っている」で片づけられたら嬉しいですよね。
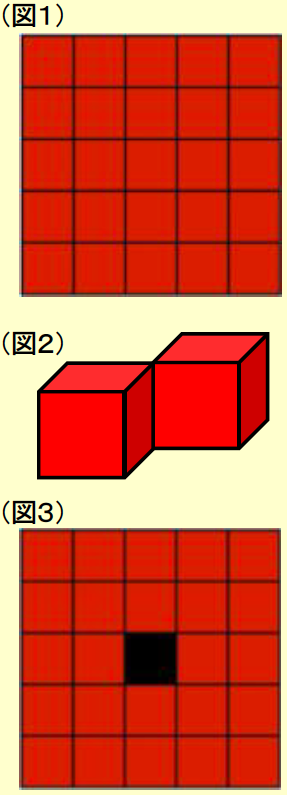一辺の長さが１ｃｍの赤い立方体が６２個、黒い立方体が１個あります。名門君は、これらを接着剤でくっつけて、大きな立体をつくろうと思いました。
目指したのは、前後左右上下６方向から見た図が全て（図１）のようになり、その中で表面積が最大になる立体です。
まずは、赤い立方体だけを使って立体『Ｐ』を作りました。下から１段ずつ５段目まで立方体を組みましたが、２段目は１３個の立方体を使用し、全体では６２個を使い切りました。立方体同士を接着するときは、その全てを（図２）のように辺と辺が重なるようにし、面と面は重ならないようにしました。立体『Ｐ』は対称性のある美しい立体でした。
ところが、表面積を求めてみるとあまり大きくなかったので、立体『Ｐ』から立方体を６個取り除いて表面積を大きくしようとしたところ、貫通して向こう側が見えてしまいました。向こう側が見えないようにするため、黒い立方体１個を頂点と頂点で接着して立体『Ｑ』を作りました。
立体『Ｑ』を前後左右上下６方向から見た図は全て（図３）のようになりました。
（１）Ｐの表面積を求めてください。
（２）Ｑの表面積を求めてください。
